
With the advent of quantum computing, the security of many classical cryptographic systems is at risk. Traditional encryption methods like RSA and ECC (Elliptic Curve Cryptography) rely on mathematical problems that are computationally infeasible for classical computers to solve. However, quantum computers, once fully developed, have the potential to break these systems by efficiently solving these problems. Post-Quantum Cryptography (PQC) refers to cryptographic algorithms that are designed to be secure against both classical and quantum computing threats.
Introduction to Post-Quantum Cryptography
Quantum computers leverage principles of quantum mechanics, such as superposition and entanglement, to perform calculations much faster than classical computers. This ability could render current encryption methods obsolete, as quantum computers can efficiently solve problems like integer factorization (used in RSA) and the discrete logarithm problem (used in ECC), which would compromise the security of data.
Post-Quantum Cryptography aims to develop cryptographic algorithms that are resistant to the power of quantum computation. These new algorithms are intended to secure sensitive information against future quantum threats, ensuring that cryptographic systems can remain secure even as quantum computing evolves.
Quantum Threats to Classical Cryptography
a. Shor’s Algorithm
Shor’s algorithm is a quantum algorithm that can efficiently factor large integers and compute discrete logarithms in polynomial time. These problems, which are the foundation of popular cryptographic algorithms like RSA, DH (Diffie-Hellman), and ECC, would be easily solvable by a quantum computer using Shor’s algorithm, rendering these systems insecure.
b. Grover’s Algorithm
Grover’s algorithm provides a quadratic speedup for unstructured search problems, including brute-forcing symmetric key encryption schemes like AES (Advanced Encryption Standard). Although Grover’s algorithm does not break symmetric encryption directly, it could reduce the security of encryption schemes by halving the effective key length (for example, a 256-bit key would provide the security equivalent to a 128-bit key).
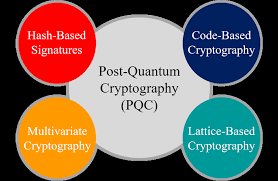
3. Approaches to Post-Quantum Cryptography
Post-Quantum Cryptography encompasses several approaches to create quantum-resistant cryptographic algorithms:
a. Lattice-Based Cryptography
Lattice-based cryptography is one of the most promising areas of post-quantum cryptography. Lattice problems are believed to be difficult for both classical and quantum computers to solve. Algorithms based on lattice problems include:
- NTRU (N-th Degree Truncated Polynomial Ring): A public-key encryption system that is resistant to quantum attacks.
- FrodoKEM: A key exchange protocol that relies on the hardness of the Shortest Vector Problem (SVP) in lattices.
b. Code-Based Cryptography
Code-based cryptography is based on the hardness of decoding a random linear code. These systems are believed to be resistant to quantum attacks, and some well-known examples include:
- McEliece Encryption: A public-key encryption scheme that has been around since the 1970s and remains secure against quantum attacks.
c. Multivariate Polynomial Cryptography
Multivariate cryptography relies on the difficulty of solving systems of multivariate polynomial equations over finite fields. Some cryptographic schemes, such as:
- Rainbow Signature Scheme: A digital signature scheme that uses multivariate polynomials, providing post-quantum security.
d. Hash-Based Cryptography
Hash-based cryptography uses hash functions to create secure digital signatures. These signatures are based on the properties of hash functions, which are believed to be resistant to quantum attacks. One such example is:
- XMSS (eXtended Merkle Signature Scheme): A hash-based signature scheme that offers long-term security against quantum threats.
e. Isogeny-Based Cryptography
Isogeny-based cryptography leverages the difficulty of finding isogenies between elliptic curves. These systems provide an alternative to traditional elliptic curve cryptography and are seen as a promising avenue for post-quantum cryptographic algorithms.
- SIKE (Supersingular Isogeny Key Encapsulation): A key encapsulation mechanism based on isogenies between supersingular elliptic curves.
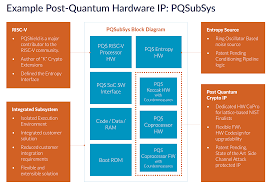
Standardization Efforts for Post-Quantum Cryptography
The need for secure cryptographic systems that can withstand quantum attacks has led to global initiatives, with the most notable being:
- NIST Post-Quantum Cryptography Standardization Project: The National Institute of Standards and Technology (NIST) has been working on standardizing post-quantum cryptographic algorithms. After multiple rounds of evaluation, NIST has selected several algorithms for further standardization, including lattice-based schemes (such as Kyber for public-key encryption and NTRU), code-based schemes (like McEliece), and hash-based signature schemes (XMSS and SPHINCS+).
This standardization process aims to establish widely adopted quantum-resistant cryptographic standards for securing communications, digital signatures, and other data security applications.
Challenges in Post-Quantum Cryptography
Despite the progress in developing post-quantum algorithms, there are several challenges to overcome:
- Efficiency: Many post-quantum cryptographic schemes, particularly lattice-based and code-based systems, tend to be more computationally intensive than classical systems. For widespread adoption, these systems need to be optimized for performance in terms of speed, storage, and bandwidth.
- Key Sizes: Quantum-resistant algorithms often require significantly larger key sizes compared to classical systems, which could lead to higher computational overheads.
- Interoperability: Transitioning from classical cryptography to quantum-resistant systems will require careful planning, as it involves upgrading existing infrastructure and ensuring compatibility between old and new systems.
Conclusion
Post-Quantum Cryptography is a crucial area of research and development as we approach the era of quantum computing. The potential of quantum computers to break classical encryption methods poses a significant threat to the security of digital systems. However, the development of quantum-resistant cryptographic algorithms promises to safeguard sensitive information in a quantum future. As NIST and other organizations continue to finalize standards and algorithms, the transition to post-quantum cryptography will be an essential step in ensuring long-term cybersecurity.
